>>Theoretical Physics>Multislit>Multislit 0.1.5b & 0.1.6b>Theory
Multislit Gauss Beam Theory
Fresnel Propagation Fresnel-Propagation

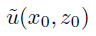We are starting in a more general context with a one-dimensional, reduced field amplitude with lateral coordinate 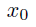at fixed longitudinal coordinate 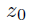. We want to propagate the field to the coordinates 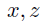, namely to the reduced field 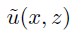. We do this by Fresnel approximation of Huygen's integral: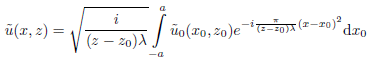

which is the convolution of 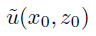with the fresnel propagator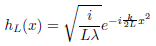

for the propagation length L. 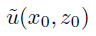		Wir beginnen in einem etwas allgemeineren Kontext mit einer eindimensionalen, redizierten Feldamplitude mit lateraler Koordinate 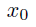an fester longitudinaler Koordinate 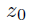. Wir möchten das Feld zu den Koordinaten 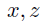propagieren, nämlich zum reduzierten Feld 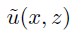. Wir setzen dies durch die Fresnel-Approximation des Huygensschen Integral um: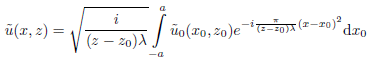

welches die Faltung von 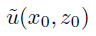mit dem Fresnel-Propagator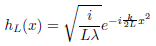

für die Propagationsdistanz L darstellt.

The Problem Das Problem

The initial reduced field amplitude shall be unity, i.e., we are constraining ourselves to an incident planar wave propagating parallel to the longitudinal axis. The field will be cut off by the apertur. The aperture shall be an infinite slit, a rectangle function of width 2a in x. We introduce unitfree coordinates

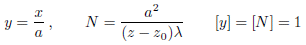
N is the Fresnel number of the slit, and y is the reduced transversal coordinate x taking unity at the edges of the slit. Then the Fresnel integral becomes

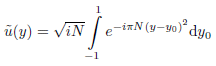
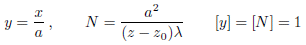
This integral is to be solved. 		Die anfängliche reduzierte Feldamplitude sei eins, d.h. wir beschränken uns auf eine einfallende ebene Welle, welche sich parallel zur longitudinalen Achse ausbreitet. Das Feld wird durch die Apertur abgeschnitten werden. Die Apertur sei ein unendlich langer Spalt, eine Rechteckfunktion der Breite 2a in x. Wir führen einheitenlose Koordinaten ein:

N ist die Fresnel-Zahl des Spaltes, und y ist die reduzierte transversale x-Koordinate. y ist an den Kanten des Spaltes eins. Dann wird das Fresnel-Integral:

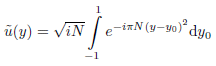
Dieses Integral soll gelöst werden.

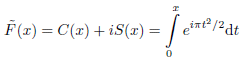
The complex Fresnel integral Das komplexe Fresnel-Integral

The complex Fresnel integral is defined to be

with


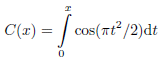
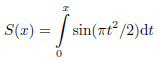
For the Fresnel integral holds

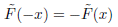
There exist analytical approximations for the Fresnel integral

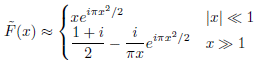
where the second one holds according to Siegman also for values of x only slighter greater than unity. But for the transition region between the two regimes, no analytical approximation exists.
But Abramowitz and Stegun give a purely empirical rational approximation to the Fresnel integral, using

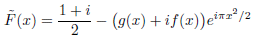
with


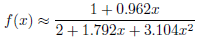
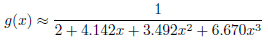
The error of this approximation is 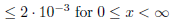, but Siegman does not tell whether absulute or relative.
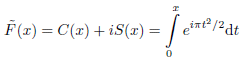
Minor caveats against the validity of this approximation arise when looking at the examples, but the overall perfomance of the formula seems to be very precise and very good. 		Das komplexe Fresnel-Integral is definiert als

mit


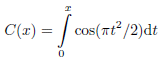
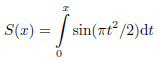
Für das Fresnel-Integral gilt

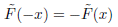
Es existieren analytische Annäherungen des Fresnel-Integrals

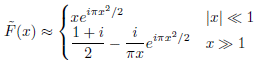
wobei die zweite laut Siegman bereits für Werte von x nur leicht größer als Eins bereits gut zutrifft. Aber für den Übergangsbereich zwischen den beiden Regimen existiert keine analytische Approximation.
Jedoch geben Abramiwitz und Stegun eine rein empirische rationale Näherung des Fresnel-Integrals unter Benutzung von

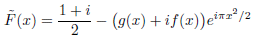
mit


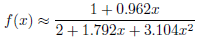
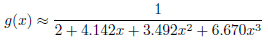
an. Der Fehler dieser Approximation ist 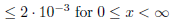, wenn auch Siegman nicht mitteilt, ob absolut oder relativ.
Untergeordnete Einwände gegen die Gültigkeit der Approximation tauchen bei Betrachtung der Beispiele auf, aber die Gesamtleistung der Formel schein sehr präzise und sehr gut zu sein.

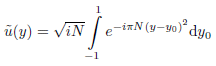
Application to the Single Slit Anwendung auf den einfachen Spalt

We have obtained earlier for the integral describing the diffraction by a single slit in the paraxial approximation

Setting

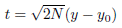
equivalent to

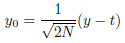
the transformation is

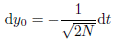
and for the integral holds thus

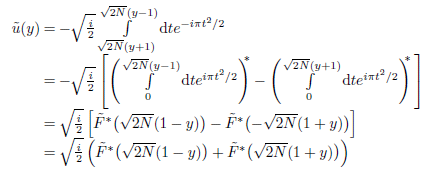
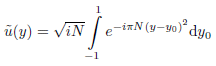
The single slit integral is now expressed in terms of the Fresnel integral, for which the rational approximation by Abramowitz and Stegun is applicable. 		Für das Integral, das die Beugung an einem einfachen Spalt in der paraxialen Näherung beschreibt, haben wir weiter oben erhalten:

Setzen wir

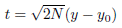
äquivalent zu

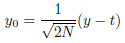
so ist die Transformation

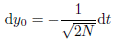
und für das Integral gilt damit

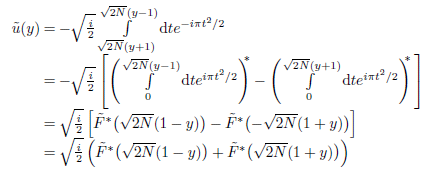
Das Integral des einfachen Spalts ist nun in Termen des Fresnel-Integrals ausgedrückt, für welches die rationale Approximation von Abramowitz und Stegun anwendbar ist.

Literature Literatur

This treatise of the single slit is based on:

Anthony E. Siegman: Lasers
Sausalito, California: University Science Books, 1986
Pages 716--726 		Diese Abhandlung des einfachen Spalts basiert auf:

Anthony E. Siegman: Lasers
Sausalito, California: University Science Book, 1986
S. 716--726

Multiple Slits Mehrfachspalte

Parallel Slits Parallele Spalte

When considering multiple parallel slits, the problem is still one-dimensional. A lateral shift of a single slit can be interpreted as the same concern as the centered singe slit by moving the frame of reference into the center of the shifted slit. As the impinging light shall be a coherent planar wave with wave front perpendicular to the z axis, the illumination is transverse translation invariant.
The computation for a single slit delivers to us a full fledged field, with amplitude (in the meaning of absolute value) and phase. As the field theory underneath is linear, coherent radiation components from different sources add up linearly. Thus, computing multiple slits is nothing more complicated than summing over evaluations of the formula for a single slit at different y positions. 		Bei der Betrachtung mehrerer paralleler Spalte ist das Problem immer noch eindimensional. Eine laterale Verschiebung eines einfachen Spalts kann als derselbe Gegenstand wie der zentrierte einfache Spalt interpretiert werden, indem das Referenzsystem in das Zentrum des verschobenen Spaltes verlegt wird. Da das einfallende Licht eine kohärente ebene Welle mit Wellenfronten senkrecht zur z-Achse sein soll, ist die Beleuchtung transversal verschiebungsinvariant.
Die Berechnung für den einfachen Spalt liefert uns ein voll ausgebildetes Feld, mit Amplitude (im Sinne von Absolutwert) und Phase. Da die Feldtheorie darunter linear ist, addieren sich kohärente Komponenten von verschiedenen Quellen linear auf. Damit ist die Berechnung mehrfacher Spalte nichts Schwierigeres als die Summation über Auswertungen der Formel für den einfachen Spalt an verschiedenen y-Positionen.

Perpendicular Arrays of Slits Senkrechte Anordnung von Spaltgruppen

When the diffracting aperture is separable, the 2D diffraction formula separates into two one-dimensional diffraction integrals of the shape we encountered. This is due to the addition law of the phasors, which in turn are only grouped by sum signs. The reader can thus easily obtain the full diffraction integral by multiplying two one-dimensional integrals as given here, pulling the factors under a common integral sign, and inducing to the more general field amplitude with arbitrary, non-separable coordinate dependencies.
Thus the computation of the diffraction signal of two crossed one-dimensional apertures is nothing more than the complex product of their single diffraction fields. 		Wenn die Beugungsapertur separabel ist, separiert das 2D-Beugungsintegral in zwei eindimensionale Beugungsintegrale von der Form, der wir hier begegnet sind. Dieses Verhalten liegt im Additionsgesetz der Phasoren begründet, welche eben gerade bloß durch Summenzeichen verknüpft sind. Der Leser kann daher einfach die ganze Beugungsgleichung erhalten, indem er zwei eindimensionale Integrale multipliziert, wie sie hier gegeben wurden, die Faktoren unter ein gemeinsames Integralzeichen zieht, und zu einer allgemeineren Urfeldamplitude induziert mit beliebiger, nicht-separierbarer Koordinatenabhängigkeit.
Somit ist die Berechnung des Beugungssignales zweier gekreuzter eindimensionaler Aperturen nicht mehr als die Bildung des komplexen Produkts ihrer einfachen Beugungsfelder.

Examples (500k pictures)Beispiele (500k-Bilder)

Files and documentationDateien und Dokumentation

Maintained since: 7/09
$Last changed: 7/09$
Impressum/Contact